下町データサイエンティストの日常

下町データサイエンティストの成果物

傾向スコアを用いた因果推論入門~理論編~

0. はじめに

最近因果推論を勉強したので、アウトプットとしてブログにまとめます。
本記事ではRubinの反実仮想 / 傾向スコアの話をしたいと思います。 具体的には、傾向スコアを使って因果推論を行う上で最低限知らなくちゃいけないことをまとめました。
私は別に統計ガチ勢でもないので、間違った見解について書いている可能性もありますので、多めに見ていただけばと思います。
また、以下でRubinと書いてあるものは、おおよそこの論文のことを指していると解釈してください。

central role of the propensity score in observational studies for causal effects | Biometrika | Oxford Academic

本ブログで紹介する傾向スコアを用いた分析の全体像は以下の図のようになります。
各フェーズについて、「どんな事をしているか」「何を用いて正しいと評価するか」「注意すべきポイントはどこか」について書いていければなぁと思います。 f:id:pira_nino:20190616163743p:plain

また、本来は実装もこの記事で収めようとしましたが、あまりにも長すぎるので別記事で切り出します(苦笑)
最低限の説明だけで、2万5千字、、、、因果推論難しいですね。。。(苦笑)

実装編は追々公開します。

1. 因果推論~施策の本当の効果~

1.1 TVのCMを見るとアプリのプレイ時間が短くなる！？

実例から入った方がイメージつきやすいので、理論の説明よりも実例から入ります。
あなたは某アプリを扱う会社のマーケターだとします。アプリのプレイ時間をあげるために、テレビCMを流す施策を実行しました。今回の分析の目的は「アプリのテレビCMを流すことで、アプリのプレイ時間が伸びるか」を検証することです。
しかし、実際にCMを見た人 / 見ていないない人のデータを集計してみると、「プレイ時間：CNを見た人 < CMを見ていない人」という分析結果が得られました。
この結果を素直に受け取ると、「アプリのCMはユーザのやる気を削ぐダメダメCMだった」「CMは見せない方がいい。CM施策は失敗だった」という結論になってしましまう。

これは本当でしょうか？？
マーケティングをかじっている勘のいい方は気が付いていると思いますが、この実例にはトリックがあります。「CMを見ている人の多数は年齢層が高い / マホの利用頻度が低い人が多く、そもそものアプリのプレイ時間が短い」という背景があります。
この背景を踏まえると「単純にCMを見た or 見ていないで差を比較することは、あるべき姿ではないのでは？」ということに気がつくと思います。

このように、「施策を行なったから本当に効果があったか」の分析を行うことが因果推論の大きな目標となります。

f:id:pira_nino:20190615153247p:plain

1.2じゃぁ理想的な比較方法は？

単純に見た or 見ていないで比較を行うことはダメであることは分かりました。では、どのような人同士を比較するべきか考えてみましょう。
理想としては、「背景要因が同じデータ間でCMを見たor見ていないで比較したい」ことは明らかでしょう。ここでいう背景とは、年齢や性別、そもそものアプリの使用時間などを意味します。これらの条件が同じデータで「CMを見たor見ていない」でCMを見た後のアプリのプレイ時間を比較することが望ましいでしょう。
そこで、背景要因を{x}、施策を受けたか(例：CMを見たor見ない)のフラグ0 or 1をz、測りたい効果である目的変数(例：アプリのプレイ時間)をyで定義します。
さらに、z=1つまり、施策を受けた群をテスト群、z=0つまり、施策を受けていない群をコントロール群と定義します。
ちなみに分野では、{x}を共変量(covariate)、zを割り当て(treat)と呼びます。*1
因果推論の目標は、「割り当てzを受けるor 受けないで目的変数yの差がどれくらい生じるかの効果測定」となります。
本記事では、この効果のことを「因果効果」と定義します。

f:id:pira_nino:20190616180103p:plain

話は戻り、「背景要因を揃えた上で比較を行う」ことは以下のように解釈できます。

  • テスト群とコントロール群で類似度の高い{x}を持ったサンプルを抽出
  • そのデータ同士でyを比較する

これを行うことで、背景要因が揃ったデータ間での割り当ての効果を測ることができます。
しかし、これを実現するために多くの問題がありますので以下で紹介します。

1.3 背景要因を揃えた比較が難しい問題

f:id:pira_nino:20190706205919p:plain

(1)共変量の次元が大きいと類似度計算が難しい
機械学習勢にはよく当たる問題ですが、共変量の次元が大きくなると単純にユークリッド距離でデータ間の距離を測ることはナンセンスであることが知られています。 次元の呪いの話もそうですが、直感的に距離計算が面倒な匂いがすることは同意できると思います。 ちなみにマハラノビス距離を用いて類似度の高いテスト / コントロール群から類似度の高いデータを抽出し、効果を測定している事例もあります。
このように、共変量の次元が大きくなると類似度の高いデータを探すとは一筋縄ではいきません。

(2)そもそも「ランダム化比較試験」すれば良いのでは？
「ちゃんと(20代男性 / スマホ使用時間10時間)の人を100人ずつ、(50代女性 / スマホ使用時間5時間)の人を30人ずつ均等にA群B群に分けるといったような、テスト群 / コントロール群の共変量を揃えたABテストの設計を行う」という方法が思いつくと思います。
このように、テスト群 / コントロール群間の施策の効果測定の際に、偏り(=バイアス)もない実験のことをランダム化比較試験(RCT)と呼びます。
もちろん、このようにRCTが仮定できるように施策の割り当てを行うことが最も理想です。しかし、現実はそうもうまくいきません。
TV CMの施策を考えると、意図的に施策の割り当て先をコントロールできないので事実上RCTは不可能です。例えば、同じ20代男性という共変量を持つAさんにはCMを見せつつ、BさんにはCMを見せないようにすることはコントロールできません。
余談ですが、TV CMの例では確かにRCTは不可能ですが、「youtubeの広告を誰に見せるか」などの実験は意図的にテスト群 / コントロール群の共変量の条件を揃える実験ができるかもしれませんね。 実務的にはRCTの実現が可能であれば、しっかりテスト / コントロール群の設計を行いABテストを行なった方が、因果推論を用いた分析を行うよりも安全です。

(3)そもそもテスト / コントロール群にしか存在しないデータがある = バイアスがある
後述の反実仮想的な因果推論として注目すべきは(3)です。 上記の例では、スマホ派の人はそもそもTVを見ないのでコントロール群に多く存在していることについて触れました。(2)の話にも重複しますが、スマホ派の人はそもそもテスト群にいない可能性が高いです。こうなると理想的な比較が難しいことは自明です。
別の事例を考えて見ましょう。ある新薬を与えた結果、病気が治ったかの検証を考えます。病気持ちのAさんに薬を与えたら健康になったデータが存在するとします。この際に薬の効果を測る上では、「仮にAさんが薬を与えなかった際の健康度合い」と比較すべきでしょう。しかし、Aさんは現に薬を与えられたので、「仮に与えなかった」という状況の再現は不可能です。このように「仮にxxxしなかったら」の再現が難しい事象は医学 / 生物の実験で多く発生します。これゆえに医学 / 生物の分野では因果推論が多く用いられています。加えて経済系でも因果推論が多く用いられています。
このように多くの実験において、テスト / コントロール群のデータに偏りが生じているので、事実上同じ条件を持ったテスト / コントロール群のデータによる比較は難しいことが知られています。

1.4 反実仮想：仮に「xxxしたら / しなかったら」の効果算出

テスト群 / コントロール群で共変量が揃ったデータがないならば、割り当てあり(z=1)のデータに対して「仮に割り当てなし(z=0)だったら」、割り当てなしz=0のデータに対して「仮に割り当てありz=1だったら」を考えることを反実仮想と呼びます。この「もしxxxxだったら」を考え効果を測定することがRubinの因果推論の本質です。 イメージとしては、「CMを見たAさんが仮にCMを見ていないならばアプリのプレイ時間はどうなったか？」を算出するイメージです。 y_1を割り当てを受けたときの目的変数、y_0を割り当てを受けないときの目的変数*2とすると、求めたい割り当ての効果 / 因果効果はE(y_1) - E(y_0)と書けます。

2. 傾向スコアを用いた効果測定

これらの背景を踏まえて産み出されたのが傾向スコア。 ここからの話を簡単に説明するとこんな感じです。

テスト群のあるデータに対して似たコントロール群のデータを持って来れば反実仮想的な推定ができる。
でも、共変量が多次元だと類似度の測定難しいしななぁ。。。
そうや「SUTVA」と「強く無視できる割り当て条件」が仮定できているならば、傾向スコアの似ているデータが「仮にxxxしなかったら」のデータとしてok。
傾向スコアが近いテスト / コントロール群のデータ同士をマッチングさせて比較すれば、割り当ての効果が算出できる。

というわけで、それぞれの要素について説明していきます

2.1 絶対にこの条件は守ろう ~ 「SUTVA」/「強く無視できる割り当て条件」~

Rubinの反実仮想を用いた因果推論を行う上では「SUTVA」と「強く無視できる割り当て条件」について絶対に満たされている必要があります。これらの2つの条件について簡単に説明します。

2.1.1 SUTVA

SUTVA(Stable Unit Treatment Value Assumption)条件。下記にRubinのお言葉をそのまま引用します。

SUTVA is simply the a priori assumption that the value of Y for unit u when exposed to treatment t will be the same no matter what mechanism is used to assign treatment t to unit u and no matter what treatments the other units receive.

噛み砕くいた解釈を行うと、「各要素の目的変数はに各要素に干渉せず、独立である」という感じです。例えばテスト群の人気Youtuber AさんがCMを見た結果、市場全体がアプリの利用時間が長くなるなど、「他人の結果が他人に影響を出すのはダメ」といった仮定です。

https://amstat.tandfonline.com/doi/abs/10.1080/01621459.1986.10478355#.XSCQ-JP7Qmo

2.1.2 強く無視できる割り当て条件

因果推論初学者の鬼門 強く無視できる割り当て条件(Strongly Ignorable Treatment Assignment)。(少なくとも私は躓いた。。。)
ずばり数式で書くと以下である。

(y_1, y_0) \perp z | {x}

数式をパッと見で理解できた方はいいのですが、初学者はここでつまづくと思います。
素直に数式を読み解くと、「共変量{x}が同じであれば、割り当てzと目的変数(y_1, y_0)の同時分布は独立」となる。
自分なりに噛み砕いた解釈を以下に書きます。

  • 割り当てがされる確率は、あくまでも共変量のみに依存し、目的変数には依存しない
  • 例えば、年齢 / 性別 / 普段のTVの視聴時間などの共変量のみが、CMを見るかに依存する
  • つまり共変量(年齢性別など)が同じ個体であれば、割り当て(CMを見る)される確率P(z)は同じ。

この条件が成り立てば、同じ共変量{x}を持つデータであれば、割り当てzのみで、目的変数y_1, y_0の効果が変化すると解釈できます。
一方、この強く無視できる割り当て条件が最も因果推論を厄介にしている厳しい条件です！！例えば、同じ性別年齢であれば、CMを見る確率は全データにおいて同じといった仮定を置いていると解釈できます。「この条件ってめちゃくちゃ厳しくね？」って思いますよね。でもこれを仮定しないと以降の話に入れないんですよ。この条件を満たしているかの確認は絶対に必要です。

2.1.3 どうやって条件が成り立ってるか確認するの？

残念ながらこの手法を使えば条件が成り立っていると証明できる便利な手法はありません。データの過程を考える、共変量を見直すなど、「データと向き合う」しか解決方法はありません。
特に、「強く無視できる割り当て条件」については厄介です。本当に今の共変量{x}で、割り当てzと目的変数(y_1, y_0)の同時分布は独立かは常に気をつける必要があります。割り当て以外に、「共変量として考慮していない背景要因のせいで目的変数が影響を受けている」というのがあるあるパターンです。
因果推論では強く無視できる割り当て条件が成立しないと正しい因果が得られないので、絶対に守る必要があります。その為にはデータに対し徹底的に向き合う必要があります*3。

2.2 傾向スコアe(x)とは

ちょっと数式が続きます。
強く無視できる割り当ての元で、効果 E(y_1 - y_0)をゴニョゴニョ式展開していきます。(最後の展開は強く無視できる割り当てを用いている)

\begin{aligned} E(y_1 - y_0) &= E(E(y_1 - y_0|x)) \\ &=E(E(y_1|x) - E(y_0|x))\\ &=E_x[ E(y_1|z=1,x) - E(y_0|z=0,x) ] \end{aligned}

下記ブログから引用を行うとこの式はこのように解釈できます。

この式の左辺は，因果効果です．最後の等号は強く無視できる割り当ての仮定から成立します．この式の意味は，処置群と対照群で同じ共変量xを持つ標本の平均を計算した後に，その差を計算するという操作を，すべてのxで平均することができれば，平均処置効果は求めることができるという意味です．もっとわかりやすく（厳密さを欠いて言えば），「各共変量の値について，その値を持つ標本を処置群・対照群から選び出し，その標本の結果変数の差を計算するという操作を，すべての共変量の取りうる値について平均化すればいいんだ」と言っています． これは，つまり，どちらの群に割り当てのかを決める共変量xの値が等しい標本ごとの差を計算せよ！と言っています．つまり，その共変量を固定した箇所で見れば，標本はランダムに割り当てられていることになります．なので，これが処置の効果になるんです．

tomoshige-n.hatenablog.com

さらに、Rubinは共変量{x}の関数b({x})で、その値で条件つければ{x}と割り当てzが独立になる関数を「バランシングスコア」と定義しました。このバランシングスコアとして最も単純な関数がP(z|{x})を意味する傾向スコアe(x)です。

x \perp z | b( {x} )

強く無視できる割り当て条件の元で再び式変形をゴニョゴニョすると、以下が成り立つことが証明されています。詳しい式展開の日本語の資料ですと、以下が分かりやすいです。

https://hoshinoseminar.com/pdf/2018_SUUMO.pdf

(y_1, y_0) \perp z | b( {x} )

さて、この式より上の期待値の式の{x}をb({x})の代表例のe(x)で置き換えると、

E(y_1 - y_0) =E_{e(x)}[E(y_1|z=1,e(x)) - E(y_0|z=0,e(x)) ]

となります。この式は、「求めたい効果は傾向スコアが等しいところでの群平均の差をとって、傾向スコアで期待値とったもの」と解釈できます。
なんのこっちゃですが、ざっくり使い道を説明すると、「テスト / コントロール群で同じような傾向スコアを持つデータペアを作って、目的変数yの差の平均が効果」という解釈になります*4。というかこれが傾向スコアを使ったマッチングの背景になります。

まぁそんなことはさておき、今北産業*5で説明すると

  • 傾向スコアe(x)：P(z=1|x)。xの元で割り当てっぽい確率
  • 強く無視できる割り当て条件の元で、似た背景を持つデータであることの指標として傾向スコアを用いる
  • 求めたい効果：テスト群のe(x)に近いコントロール群のデータのペアを作り、ペア間の目的変数yの差の期待値

反実仮想的に考えると、あるテスト群のデータに対し同じ傾向スコアを持つコントロール群データを「もし割り当てがなかったときのデータ」とすると解釈できます。

f:id:pira_nino:20190615213302p:plain

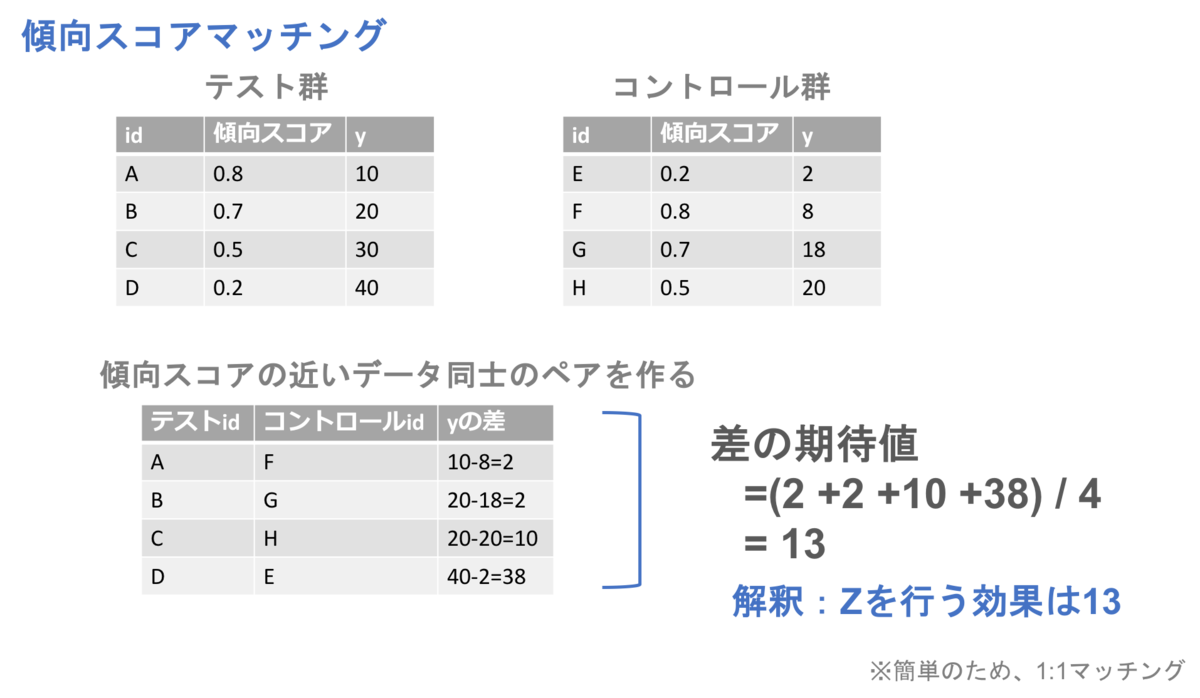
3. 傾向スコア算出

モデリング → 評価の2ステップに分けます。
特に評価については、色々思うところがあるので長々書きます。

f:id:pira_nino:20190615222726p:plain

3.1モデリング

共変量xから割り当てzを予測する2値分類モデルを構築するフェーズです。
個人的にはどのモデルでもいいと思っています。統計系の人がの主戦場であるからか多くの論文ではロジットモデルを使っていますが、別にはRFやLightGBMなどの機械学習手法を用いてもいいのではと思っています。

3.2モデルの評価

これが一筋縄ではいきません、、、 、
下記の評価方法を見て、怪しいところがあればモデリングの見直しや共変量の再検討を行うべきです。

(1)c統計量
機械学習的にいうAUCです。多くのブログなどでは「c統計量が0.7以上ならok」という記述が書かれていますが、個人的には懐疑的です。
そもそも傾向スコアを用いた分析(特にマッチング)では、「反実仮想的にもし割り当てがなかったらとするデータの類似度を傾向スコアで測る」ことが目標なので、「テスト / コントロール群での傾向スコア自体の分布」や、「傾向スコアが同じ値をとるデータ間の共変量の分布」の方が大切でだと私は考えています。
また、以下のマッチングの歴史についてまとめた論文にも「c統計量ではなく、共変量のバランスを評価すべき」という旨が書かれております。

The model diagnostics when estimating propensity scores are not the standard model diagnostics for logistic regression or CART. With propensity score estimation, concern is not with the parameter estimates of the model, but rather with the resulting balance of the covariates (Augurzky and Schmidt, 2001). Because of this, standard concerns about collinearity do not apply. Similarly, since they do not use covariate balance as a criterion, model fit statistics identifying classification ability (such as the c-statistic) or stepwise selection models are not helpful for variable selection (Rubin, 2004; Brookhart et al., 2006; Setoguchi et al., 2008). One strategy that is helpful is to examine the balance of covariates (including those not originally included in the propensity score model), their squares, and interactions in the matched samples. If imbalance is found on particular variables or functions of variables, those terms can be included in a re-estimated propensity score model, which should improve their balance in the subsequent matched samples (Rosenbaum and Rubin, 1984; Dehejia and Wahba, 2002).

Matching methods for causal inference: A review and a look forward

もちろんモデルの最低限の精度を見る指標として、AUCを見ることは必要です。しかし、AUC>0.7だからなんでもokという考え方は危険だと思います。
余談ですがc統計量を批判している論文もあります汗

The role of the c-statistic in variable selection for propensity score models

(2)テスト / コントロール群の傾向スコアの分布
仮に、傾向スコアが正しく振れているならば

  • 傾向スコア0.1 (テスト群のデータ：コントロール群のデータ) = 1 : 9
  • 傾向スコア0.5 (テスト群のデータ：コントロール群のデータ) = 5 : 5
  • 傾向スコア0.9 (テスト群のデータ：コントロール群のデータ) = 9 : 1

の割合でデータが存在するはずです。
これは、上の図のように傾向スコアのヒストグラムがテスト / コントロール群で左右対象になっていることを意味します。
定量的に評価を行う方法はありませんが、見ておいた方が良い指標でしょう。

(3)共変量に傾向スコアの逆数を掛けた際に、テスト / コントロール群の分布が平らに補正されるか
ほぼ(2)と同じことを意味しますが、反実仮想的に共変量の背景を揃えるという意味を直接的に解釈すると、「共変量に傾向スコアの逆数を掛けた際に、テスト / コントロール群の分布が平らに補正されるか」であることは明らかです。
では、「どの変数について確認すべきか？」を考えます。もちろん全ての共変量に対して確認をするのが理想ですが現実的には次元が大きく不可能です。このような場合は重要な共変量についてチェックすれば良いと思います。重要な共変量とは、目的変数yに効く変数や、傾向スコアモデリングに効く変数のことを指します。適当なTree系のモデルや正則化を用いたロジットモデルなどを用いて算出してください。
このように、傾向スコアの逆数を用いてこの変数を補正した分布が平らになるかを確認することは因果推論において重要と考えられます。
また、この項についてはマッチングの際に「本当に似た共変量の値をとったデータペアでマッチングできているか」を評価する指標であるStadard Differenceでも分析を行います。

(4)交差検証で上記の過学習していないかの確認？
(4)は完全に私個人の見解です。
真のあるべき傾向スコアを求める上では交差検証を行う(以下、cvを切る)必要があると思っています。特に後述するIPWやダブルロバストでは傾向スコアに確率分布であることが重要な仮定であるため、必須であると考えています。
例えば、cvを切った際に(学習データのテスト群のデータ)と(評価データのテスト群のデータ)の傾向スコアに差があるかを見るべきなのでは？と考えております。
一方で、因果推論では「過去の事例に対しての割り当ての効果」を分析する問題設定なので、あまり「真のデータ」といった概念は気にしなくてもいいのかなぁとも思ったりしています。。。
あまり深く調べきれていませんが、事例も見つからなかったので強者の方ご指摘を頂けると幸いです。。。。

4. 傾向スコアを用いたマッチング

4.1 マッチングのお気持ち

テスト群の各データに対し反実仮想で「もし割り当てがなかったら」のデータを、傾向スコアが似ているコントロール群のデータとみなし比較を行うことを傾向スコアマッチングと呼びます。
傾向スコアマッチングには数種類のマッチング手法があるので、それぞれ簡単に説明します。

4.2 様々なマッチング手法

最近傍マッチング(Nearest Neighbor)
テスト群データ1つに対して最も傾向スコアが近いコントロール群のデータをマッチさせる手法です。
マッチさせた後はペアのyの差の期待値が求めたい効果となります。
最近傍法をマイナーチェンジした手法としては以下が挙げられます。

  • 1つのテスト群のデータに対し同じ距離のコントロール群のデータが複数あれば、1つのテスト群のデータに対し複数のペアを作成
  • 1つのテスト群のデータに対し、近傍M個のペアを作成する
  • 1つのコントロール群データがマッチングにしようされたら復元抽出を許す or 許さない

R使いの方であれば、Matchライブラリにこれらのオプションがあるので試してみると良いでしょう。

sekhon.berkeley.edu

caliper
最近傍マッチングでは、1つのテスト群のデータに対して最も傾向スコアが近いコントロール群のデータをマッチングさせていました。しかし、最近傍とはいえ大きく傾向スコアが異なるデータ同士がマッチングしたならば良いマッチングであるとは言えません。
そこで、最近傍法に対し、「この距離以上離れていたらマッチングさせません」という手法がcaliper制限をかけた最近傍マッチングです。
一般にcaliperを設定することは主流であり、値としては0.2程度が望ましいと言われています。あくまでも統計よりの論文の事例なので、莫大なデータ数を扱う事例ではどの程度にすれば良いか私も分かっておりません。仮に傾向スコアが「ちゃんと確率を表現できている」ならば、確率0.2以上離れているデータペアのマッチングのはナンセンスということは直感的ですね。
ちなみに、上記のRのMatchライブラリではcaliperというオプションがあり、簡単に設定することができます。 f:id:pira_nino:20190616141639p:plain

層別マッチング
テスト / コントロール群に対し、傾向スコアが「ある値以上ある値未満」のグループをK個作成し、そのグループ同士の目的変数yの値をの差の比較を行う手法。
通常、グループはK個のグループに所属するデータ数が均等になるように傾向スコアの閾値を決めてグルーピングを行います。

その他
その他の有名どころをいくつか紹介します。

  • 最適マッチング：各ペアの傾向スコアの差分(=距離)の合計が最小になるようにペアを作る
  • 遺伝的マッチング(GenMatch )：遺伝的アルゴリズムを用いて、マハラノビス距離を最小するようなペアリングを作成
  • フルマッチ(Full Mathing)：全テスト / コントロール群のデータをペアリングに使うことを目的とし、1:k、k:1マッチングを行う手法

https://www.mitpressjournals.org/doi/abs/10.1162/REST_a_00318

Using Full Matching to Estimate Causal Effects in Nonexperimental Studies: Examining the Relationship Between Adolescent Marijuana Use and Adult Outcomes

4.3 マッチングのメリット / デメリット

メリット

  • わかりやすい

  • 分析が簡単

デメリット

  • テスト群のデータサイズに依存する(特に1:1マッチ)
  • テスト群とコントロール群で傾向スコアのヒストグラムの傾向が異なれば、マッチングができない
  • マッチングに計算時間がかかる

注目すべきはデメリットの「データサイズ依存」の話です。
テスト群のデータがコントロール群に比べて少ない問題設定では、1:1マッチを行うと多くのコントロール群のデータがマッチングに用いられないので、検出力が下がることは明らかです。また、テスト群とコントロール群で傾向スコアのヒストグラムの傾向が異なれば、マッチングができるデータ数が少なくなるので、さらにデータ量の問題を重症化させます。

4.4 マッチングの評価

任意のマッチング手法を用いて、テスト / コントロール群のデータのペアリングができたました。ここでは「このマッチングはどれくらい良いマッチングであるか」を評価する手法として standardized difference (SD)を紹介します。簡単の為、全共変量が連続値である場合のSDの式を以下に示します。

SD = \frac{\bar{x}_{test} - \bar{x}_{ctr} }{\sqrt{ \frac{s^2_{test} + s^2_{ctr} }{2} }}

ここで、\bar{x}_{test}などは全テスト群のデータではなく、ペアリングに採用されたテスト群のデータであることに注意してください。(ctrも同様)
この数式のイメージとしては、「ペアリングに用いられたテスト / コントロール群のデータの共変量に差がないか」を表す指標として解釈してください。
そもそも強く無視できる割り当てを満たした元での反実仮想では、「テスト群に似た共変量を持つコントロール群のデータがマッチされるはず」ということを思い出せば、妥当な評価であることが理解できると思います。 ちなみに下記の論文曰く、「汎用的(universal)な閾値はないけど、0.1以下ならばok」と書かれています。

An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies

www.polyu.edu.hk

一方、共変量の次元が大きいと「全共変量に対してSDを一個一個算出したけど、どうすればいいんだ」という疑問には当たると思います。
多くの論文では全変数のSDを見ていますが、高々20次元程度であれば可能です。しかし、共変量が100次元になったらさすがに難しいです。
この際には原点に立ち戻り、全共変量を考慮したマハラノビス距離(正確には計量行列Mに分散共分散行列を仮定したマハラノビス距離)を各ペアに対して求める方が無難でしょう。 しかし、カテゴリカル変数があったら詰むなど単純なマハラノビス距離にも問題はあります。
個人的には、「あきらかにyに効いている共変量10個のSDを見る」ことでも良いのではと考えております。理想的には各共変量のSDを重み付けしてくれる何かの指標があればなぁと思いますが、ざっと調べた感じ見つかりませんでした。(Tree系モデルのimportanceはナンセンスだと思います)

4.5 そもそも傾向スコアをマッチングに用いるべきでないかも？

こんな論文があります。

gking.harvard.edu

ざっくり言うと、実験の状況によっては傾向スコアマッチングよりもマハラノビス距離マッチングの方が良いということを示している論文です。 日本語の解説では以下のブログが有用です。

analyticalsociology.hatenadiary.com

本論文は2016年に公開され2019年にupdatedされているように、最近でも議論がなされている分野になります。私はこの分野に精通している訳ではないので、個人の見解を述べるほどではありませんが、少なくとも「とりあえず傾向スコアを算出してマッチングで効果を測るという安易な因果推論は避けた方が良い」と考えています。前述の通り、因果推論は万能なツールではないので、実務上では各フェーズにおいてデータとちゃんと向き合う必要があると思います。

5. IPW / ダブルロバスト

傾向スコアを用いたマッチング以外の手法して知られている「IPW」と「ダブルロバスト」について説明します。

5.1 IPW

IPW（Inverse Probability Weighting: IPW)は、「傾向スコアの逆数を重みとした重み付け法を用いた推定量」です。先に数式を見た方が理解が進むと思うので、IPWを用いた\hat{E}(y_0)、\hat{E}(y_1)の定義を書きます。
まず、z=0,1の傾向スコアの逆数の重み付けをW_0, W_1で定義します。(z_iは0か1)

\begin{aligned} W_0 &= \sum_{i=1}^N \frac{1-z_i}{1-e_i} \\ W_1 &= \sum_{i=1}^N \frac{z_i}{e_i} \end{aligned}

この重みを用いると、y_0,y_1の周辺期待値の推定値\hat{E}(y_0), \hat{E}(y_1)は以下のように書けます。

\begin{aligned} \hat{E}(y_0) &= \frac{1}{W_0}\sum_{i=1}^N \frac{y_i(1-z_i)}{1-e_i} \\ \hat{E}(y_1) &=\frac{1}{W_1} \sum_{i=1}^N \frac{z_i y_i}{e_i} \end{aligned}

これを用いて、\hat{E}(y_1) -\hat{E}(y_0)が求めたい因果効果となります。
実はこの値は不偏推定量なので、データ数が多いときには信用のできる値となっています(ただし、傾向スコアが正しく推定できている前提で)。
式展開は以下のQiitaが分かりやすいです。

qiita.com

なんとなくのイメージですが、\hat{E}(y_1)は、傾向スコアの逆数をかけることで割り当て1の値の際のy_1に補正しているイメージです(\hat{E}_(y_0)も同様)。
実務的な話ですが、傾向スコアの逆数を用いているため、テスト群に傾向スコアが0.0001のデータがあるとinfに吹っ飛び詰みます。同様にコントロール群に傾向スコア0.9999なデータがあっても詰みます。アドホックですが、傾向スコアが0.05~0.95のデータのみをIPWの算出に使用するといったように、あらかじめ上下数%の削除を行うことをオススメします。これを行う場合は、傾向スコア0.9999、0.99、0.95のデータ同士で共変量の分布が変わらないかを念のため確認しておく必要があります。仮に、強く無視できる割り当てが成立し、かつ傾向スコアが真の確率を表現できているのであれば特に問題がないはずです。仮に問題があったのであれば、傾向スコアの算出などの前フェーズに1度立ち戻る必要があります。

5.2 ダブルロバスト

5.2.1 回帰モデル

ダブルロバストの話に入る前に回帰モデルの話をします。
ざっくり言うと、

  • z=1のデータのxでyを予測するモデルg_1(x) + c_1を作る = あるxのとき、割り当てがあったときのyを予測するモデル
  • z=0のデータのxでyを予測するモデルg_0(x)+ c_0を作る = あるxのとき、割り当てがなかったときのyを予測するモデル
  • 得られたモデルを用いて、以下のように式展開で因果効果を求めます
\begin{aligned} E(y_1 - y_0) &= E(y_1) - E(y_0)\\ & = E_x(g_1(x) + c_1) - E_x(g_0(x) + c_0) \\ & = E_x [ g_1(x) - (g_0(x) ] + c_1 - c_0 \end{aligned}

この式の各要素が求められれば、問題はないのですが、案の定色々問題があります。

問題1：モデルの正しさ
そもそも、z=0に対して、z=1だったときの効果を、z=1と観測されているデータのみで作ったg_1(x) + c_1で求めることを仮定しています。
強く無視できる割り当てが成り立っていれば、大丈夫なのですが「まぁそうも上手くいかないよね」ってのは直感的にわかると思います。
特により複雑な非線形なモデルを用いると、過学習的な感じで推定値が本来の効果と大きくずれる可能性が高くなります。
結局、z=0のデータに対して、仮にz=1だったら。。。を求める難しさ(逆も)という事になります。強く無視できる割り当てが成立しているなら、大丈夫なのですが、そうそう上手くはいかないという事を念頭にいれましょう。

問題2：g_1(x) = g_0(x)が成り立てばよくね？
さて、無事にg_1(x) + c_1、g_0(x) + c_0を推定できたとしましょう。しかし、上の式を見てみると、 E_x [ g_1(x) - g_0(x) ]の計算が必要であることがわかります。
意味的には、「 g_1(x) - g_0(x)のxの期待値」を計算することになります。しかし往々にして「xの分布分からん」という問題があり、これが計算できないことにはすぐ気がつきます。
そこで、「じゃぁ、g_1(x) = g_0(x)とすればこの期待値の計算なくなるやん」とも考えますが、これもかなり無理があることは明確だと思います。
この話は岩波DS vol.3のp71、調査観察データの統計科学のp52辺りに書いてあることの私なりの解釈になります。*6

5.2.2 ダブルロバスト

ダブルロバストのダブルは「(1)IPW (2)回帰モデルの2つ(ダブル)に対してロバスト」ということが名前の由来です。
2つのモデルの問題点をまとめます。

2つのモデルに共通 : 強く無視できる割り当てが厳しい
IPW : 傾向スコアが正しく推定(=あるべき確率)できている前提
回帰モデル : モデルの正しさ

強く無視できる割り当てが成立しているかは、「そもそもの問題設定の話に戻りますし、これが成り立っていると妥協して各手法の推定量を求めいるというお気持ち」の話になるので一度置いておきましょう。
IPW / 回帰モデルのどちらにも問題があるが、「どっちかが完璧であれば、E(y_1), E(y_0)の一致推定量となる」推定量がダブルロバストです。

\begin{aligned} \hat{E}^{DR}(y_1) &= \frac{1}{N} \sum_{i=1}^{N}[ \frac{z_{i}y_{i1}}{e(x_i)} + (1-\frac{z_{i}}{e(x_i)}) g_1(x_i) ] \\ &=\frac{1}{N} \sum_{i=1}^{N}[y_{i1} +\frac{z_{i} - e(x)}{e(x)} (y_{i1} - g_1(x_i)) ] \end{aligned}

ここで、z_iは0 or 1で、y_{i1}はz_i=1のデータのみに観測されていることに注意してください。（特に実装の際に注意）
上記の通り、数式的にはIPWか回帰モデルが正しいければ、この期待値をとることで一致推定量になります。また、漸近分散がIPWよりも小さくなるので、より良いという性質も持っています。詳しくは「調査観察データの統計科学」が参考として分かりやすいです。
同様に\hat{E}^{DR}(y_0)も以下のように書けます。

\hat{E}^{DR}(y_0) = \frac{1}{N} \sum_{i=1}^{N} [ \frac{(1-z_i)y_{i0}}{1-e(x_i)} +(1 - \frac{1-z_{i}}{1-e(x_i)} )g_0(x_i) ]

この式を用いて算出した\hat{E}^{DR}(y_1) - \hat{E}^{DR}(y_0)がダブルロバストによる因果効果となります。

www.ncbi.nlm.nih.gov

6. その他関連手法

傾向スコアを用いた分析手法ではないですが、個人的に好きな「Partial Dependence Plot」と「Proximityを用いたマッチング手法」について紹介します。

6.1 Partial Dependence Plot(PDP)

ざっくり言うと「ある変数をxxxだけ変化させた際の目的変数の変化量の可視化」手法です。
例えば、CMを見てない -> 見た に変化させた際の目的変数の変化量の可視化というイメージです。
理論的には、以下の手順により注目変数x_sにのみ依存してyを出力する関数 \bar{f}_s(x_s)を構築します。

  • 全変数を用いてyを予測するモデルf(x)を構築
  • 注目変数x_s (例：CMを見たか)とその他の変数x_cに分ける
  • 以下の式で注目変数x_sのみを引数とするの関数 \bar{f}_s(x_s)を作る
\bar{f} _s (x_s) = \frac{1}{N} \sum_{i=1}^{N} f(x_s, x_{c}^{(i)})

この \bar{f}_s(x_s)を用いて注目変数x_sを変化させた際の目的変数の変化量を推定しています。

dropout009.hatenablog.com

towardsdatascience.com

f:id:pira_nino:20190616211827p:plain

実はpythonで簡単に実行できるライブラリがあります。個人的には、注目変数と目的変数yの関係をさくっと可視化する際には有効であろうと思います。
一方で、注目変数と相関の高い変数があった場合にはあまり意味をなさないので、あくまでも参考値としてサクッと出せるものであるということはお忘れなく。

pdpbox.readthedocs.io

speakerdeck.com

6.2 Proximityを用いたマッチング手法

話は因果推論に戻り、傾向スコア以外の指標としてRFのProximityを用いたマッチング手法について紹介します。

Propensity Score and Proximity Matching Using Random Forest

Proximityとは
「木を構築する際にデータ同士が末端nodeで同じnodeに何回入ったか」をカウントしたものです。
これをデータ数×データ数の対象行列で表現したものを「Proximityマトリックス」と呼びます。

f:id:pira_nino:20190616221523p:plain

Proximityを用いたマッチング
ずばり、テスト群のあるデータに対してProximityが最も大きい値のコントロール群のデータをマッチングさせる手法です。
そもそものマッチングの目的は、反実仮想的には「テスト群と似ているコントロール群を持ってきてマッチングさせる」ことでした。そこで、木の末端にいるデータは類似度が高いと解釈できるので、このProximityマトリックスを用いてマッチングを行うというのがProximityマッチングのモチベーションになります。
パッケージを駆使すれば簡単に試せる手法なのですが、データ数×データ数の行列を保持する必要がある*7ので、メモリを食うというデメリットがあります。

7. まとめ

さて冒頭で貼った「傾向スコアを用いた分析の全体像」の図を再度見て見ましょう。
ここまで読んでみると以下の図の各フェーズが「「どんな事をしているか」「何を用いて正しいと評価するか」「注意すべきポイントはどこか」をある程度理解できたと思います。
本記事で紹介した傾向スコアを用い因果推論の例は、かなり初歩的な内容をまとめたです。まだまだ奥が深い分野なのでその入り口だけでも皆さんが興味を持ってくださったら幸いです。 f:id:pira_nino:20190616163743p:plain

8. 参考文献

本ブログの作成や業務で参考にした参考文献を下記に列挙します。

(1)Rubin元論
central role of the propensity score in observational studies for causal effects | Biometrika | Oxford Academic

(2)KDD2018のチュートリアル。因果推論をざっくり知る上ではわかりやすい
https://causalinference.gitlab.io/kdd-tutorial/methods.html#regression

(3)傾向スコアを用いた因果推論の全体像をまとめたスライド

www.slideshare.net

(4)傾向スコアを用いた分析としては非常に面白い事例。基礎的な背景の説明も丁寧に書いてあり参考になります。
https://hoshinoseminar.com/pdf/2018_SUUMO.pdf

(5)マッチングの歴史をまとめたサーベイ的な論文
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2943670/

(6)(5)の論文の解説ブログ analyticalsociology.hatenadiary.com

(7)傾向スコアマッチングを安易に使うべきでないという論文
gking.harvard.edu

(8)(7)の論文の解説ブログ analyticalsociology.hatenadiary.com

(9)様々な Standardized Differenceの定式化
www.polyu.edu.hk

(10)非常にタメになる資料！！自分のブログでは、推定量のばらつきに対する問題について記載していないので是非ご参考ください。 speakerdeck.com

(11)ダブルロバスト元論

Doubly Robust Estimation of Causal Effects

(12)ダブルロバスト系のサーベイ

https://www4.stat.ncsu.edu/~davidian/doublerobust.pdf

(13)岩波DS Vol.3。初学者はこの本から入門するとスムーズだと思う。 www.iwanami.co.jp

(14)岩波DS Vol.3をもう少し詳しく書いた感じ。読むべき一冊です。 www.iwanami.co.jp

(15)因果推論の書籍を中心にリンクがまとまっている hikaru1122.hatenadiary.jp

*1:普段機械学習に慣れ親しんでいる私としては、特徴量のことを共変量と呼ぶことに慣れるのに多少時間がかかりました。

*2:勿論z=1のデータに対してy_0は観測されていないので、潜在的 結果変数と表記している文献も多くあります

*3:因果推論は世間が思うほど便利なものではなく、泥臭いことを少しでも広められればと思うこの頃です

*4:正確には差の平均は期待値ではありません

*5:今来たから3行で説明してくれの意味。https://dic.nicovideo.jp/a/%E4%BB%8A%E5%8C%97%E7%94%A3%E6%A5%AD

*6:加えて誤差項\epsilonが同じと仮定する問題もありますが、自明なので省略します。

*7:上三角で十分なので、厳密にはデータ数×データ数の大きさのマトリックスを全部保持する必要はありません